屈折補正の基本

２．レンズの焦点距離と屈折力

　レンズは大きく分けると、平行光線がレンズで屈折後に一点に収束するプラスレンズと、レンズ屈折後に発散するマイナスレンズがあります。

２-１．プラスレンズの焦点と焦点距離

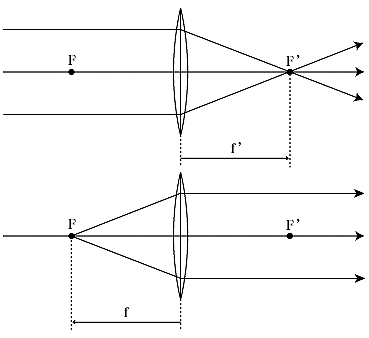
fig03
図３

プラスレンズの像側焦点と像側焦点距離
　レンズ光軸に平行に入射した光線が、レンズで屈折後、光軸上の一点に集光する点を像側焦点（f ′）といいます。また、レンズから F′までの距離を像側焦点距離（f ′）といい正の値となります。

プラスレンズの物側焦点と物側焦点距離
　レンズ光軸上のある一点（レンズ前方の点）から発散した光線が、レンズで屈折後、光軸に平行に出ていくような性質をもつ点を物側焦点（F）といいます。この物側焦点はプラスレンズの左側に存在します。また、レンズから F までの距離を物側焦点距離（f）といい負の値となります。


２-２．マイナスレンズの焦点と焦点距離

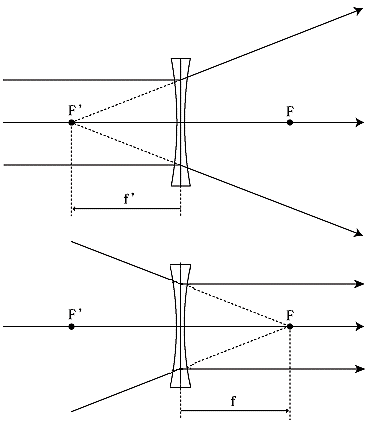
fig04
図４

マイナスレンズの像側焦点と像側焦点距離
　レンズ光軸に平行に入射した光線が、レンズで屈折後、光軸上の一点から発散する点を像側焦点（F′）といいます。また、レンズから F′までの距離を像側焦点距離（f ′）といいは負の値となります。

マイナスレンズの物側焦点と物側焦点距離
　レンズ光軸上のある一点（レンズ後方の点）に収束する光線が、レンズで屈折後、光軸に平行に出ていくような性質をもつ点を物側焦点（F）といいます。この物側焦点はマイナスレンズの右側に存在します。また、レンズから F までの距離を物側焦点距離（f）といい正の値となります。


２-３．レンズの屈折力の表し方

屈折力の定義
　レンズが光を曲げる強さを屈折力といい、屈折力が強くなるほど焦点距離が短くなります。屈折力の大きさと焦点距離は反比例するので、焦点距離 f ′(ｍ）の逆数をレンズの屈折力とします。

　凸レンズ　→　f ′＞0 なので D＞0　→　正の屈折力をもつ。
　凹レンズ　→　f ′＜0 なので D＜0　→　負の屈折力をもつ。

屈折力の単位
　屈折力の単位は、ディオプトリー（Dioptory）またはディオプター（Diopter）を用いて、通常は D で表します（SC式等で表す場合は D を省略します）。

　〈例１〉f ′＝＋50（cm）のとき →　f ′＝＋0.5（cm）→　屈折力＝＋2.00 D
　〈例２〉f ′＝−40（cm）のとき →　f ′＝−0.4（cm）→　屈折力＝−2.50 D

　必ず数字の前に符号を付けて、小数点以下第２位まで表します。



back next